método para detectar assimetria

[joao]

Ola Pessoal,

Postei aqui porque eh generico o assunto. Não estou relacionando ele a nenhuma linguagem de programação. Ok?

Minha pergunta é simples: Alguém conhece algum método para detectar assimetria? Eu gostaria mais que fosse em Código do que em algoritmo, mas qualquer um dos dois é super bem vindo!

Assimetria - De modo geral é simples de explicar: Você tem um objeto. Caso você divida ele em duas partes e as duas imagens se parecem uma imagem refletida da outra(como se estivesse vendo no espelho), então a imagem é simétrica. Senão é assimétrica. Apenas 1 porém: A imagem nunca precisa ser dividida em uma direção específica, por exemplo, na vertical ou horizontal. Ela pode ser cortada em um angulo de 53 graus que se as duas partes forem iguais, dá para considerar ela como simétrica também.

Agora o que eu preciso é apenas verificar simetria de borda. Não da imagem inteira. Exemplo: Um livro. Se você pegar o livro e dividir ele em dois, a assimetria dele provavelmente será diferente, porque as escritas e desenhos da capa não serão os mesmos. Logo o livro não é simétrico. MAS, se você pegar a borda dele, somente a borda, ele será, porque nada mais é do que um retangulo o formato do livro e um retangulo dividido em duas partes, elas serão simétricas. Espero que tenham entendido a diferença.

O que eu tenho HOJE: Uma variavél contendo 1000 pontos da BORDA do objeto. Eu só tenho isso. Então, imaginem eu scannear o livro e pegar da borda 1000 pontos(x e y) e salvar em uma variavel. É isso que eu tenho.

Qualquer ajuda é bem vinda. Idéias também! Porque estou tentando resolver este problema faz tempo.

[]'s

[marcelo_asm]

estou lendo esse livro http://www.livrariacultura.com.br/scrip ... 19F4C&uid=

é sensacional e creio que possa te interessar.

Marcelo

[joao]

Ola Marcelo_asm,

Obrigado pela dica. Mas infelizmente neste momento não tem como eu ter acesso a este livro. Teria como você explicar mais sobre ele sobre o algoritmo que tenha sobre isso? Ou se não algoritmo, a idéia por trás do livro?

Obrigado,
Joao Sauer

[fabim]

jhon..
Não sei ao certo, muito, sobre o que eu não sei se soubesse.

Mais neste caso, você vai tratar imagem digitalmente ?


ou quer apenas algo genérico ?

[]´s

fabim

[msamsoniuk]

me parece um problema relativamente simples de resolver (o que nao quer dizer computacionalmente leve)... acho que depende muito da simetria e da complexidade do objeto! de acordo com a complexidade e formato, vc escolhe uma simetria que se aplique. por exemplo, um cubo permite simetria rotacional a cada 90 graus, permite simetrias de reflexoes na horizontal e vertical, permite inversao, rotacao impropria e sabe lah mais o que. uma folha A4, por outro lado, jah nao tem os mesmos atributos de simetria, embora ainda seja um objeto bem simetrico!

uma letra "A" entao, eh algo bem mais complicado, mas tem simetria de reflexao vertical

enfim, chutando uma abordagem para alguns casos diversos, eu comecaria fazendo a somatoria dos pontos x,y,z para dividir pelo numero de pontos e obter a coordenada do ponto central do objeto, assim vc consegue ter uma referencia zerada para o objeto independente da posicao dele na imagem... a partir disso fica simples! diversas figuras regulares possuem pares de pontos simetricamente distribuidos em lados opostos do centro da figura, independente de angulo. isso eh particularmente verdade para um cubo ou folha retangular de papel.

mas no caso da letra "A", isso obviamente nao funciona! se vc fazer este mesmo teste com todos os pontos que formam a letra "A", o teste vai falhar sempre, exceto no eixo de simetria vertical! daih fechou, pq vc praticamente achou o angulo do objeto: ao inves de calcular o ponto simetrico em relacao ao centro, vc calcula o ponto simetrico em relacao ao eixo de simetria vertical e pronto, vc consegue determinar se o seu "A" eh simetrico ou nao.

obviamente o processo de digitalizacao nao cria pontos exatamente simetricos, entao vc pode partir para duas abordagens:

a) se tiver muito poucos pontos, vc pode ordenar os pontos de modo que seja possivel calcular linhas entre um ponto e outro. assim, dado um ponto de um lado, vc calcula o ponto simetrico do outro lado e mede a distancia entre o ponto e a linha. se estiver dentro de uma margem aceitavel, aquele ponto possivelmente deve fazer parte da linha de borda.

b) se vc tiver muitos pontos, basta verificar se a distancia entre o ponto amostrado e calculado esta dentro da margem aceitavel, eh pq os pontos fazem parte da mesma linha de borda.

uma outra abordagem seria fazer essa analise de modo a criar um feedback que ajusta a imagem automaticamente. por exemplo, ter na imagem alvo uma letra "A" de determinada cor, de modo a ser possivel separar na imagem apenas a letra "A" para analise. calcular o centro dela, calcular o eixo de simetria horizontal dela e, obtendo esses valores, fazer a translacao e rotacao de cada pixel da imagem de modo a obter a imagem perfeitamente alinhada!

neste caso, tendo a imagem perfeitamente alinhada e centrada, vc poderia subtrair a imagem da mesma imagem espelhada na vertical, por exemplo, obtendo assim as diferencas de simetria nao apenas na borda, mas tambem no miolo da imagem!

e por ae vai...ideias nao faltam!

[joao]

Valeu a todos pela ajuda!

Tive ajuda ateh por MSN...
A ideia realmente eh conseguir achar o ponto central e dai tracar retas e ir verificando se as imagens cortadas sao ou nao simetricas.

Valeu a todos pelas dicas.

[]'s

[MOR_AL]

Valeu a todos pela ajuda!

Tive ajuda ateh por MSN...
A ideia realmente eh conseguir achar o ponto central e dai tracar retas e ir verificando se as imagens cortadas sao ou nao simetricas.

Valeu a todos pelas dicas.

[]'s

Olá João!!

Lí ontem sua postagem, mas não tinha idéia para lhe passar.
Hoje, de relance, veio uma e acho que daria certo. Precisa conhecer a equação da circunferência no plano xy e alguma álgebra.
Segue a idéia:

1 - Escreva a equação geral da circunferência: ^ é símbolo de "ao quadrado"
(x-a)^2 + (y-b)^2 = R^2
Esta circunferência tem o seu centro no ponto P(a,b).
2 - Crie três pontos genéricos que passam pela circunferência. Obviamente possuem o mesmo raio R.
Pontos P1(x1,y1), P2(x2,y2) e P3(x3,y3).
P1: (x1-a)^2 + (y1-b)^2 = R^2
P2: (x2-a)^2 + (y2-b)^2 = R^2
P3: (x3-a)^2 + (y3-b)^2 = R^2
3 - A idéia é calcular o ponto central P(a,b) da circfunferência, dados os três pontos P1, P2 e P3.
4 - O "pulo do gato" é você escolher um ponto central P(a,b) inicial, que esteja dentro da figura. Ajude a matemática e escolha aproximadamente o ponto que você acha que é o centro da sua figura.
5 - Escolha o raio R, com cerca de 2 vezes a distância (estimada) que você imagina ser o ponto da figura mais afastado do centro de sua circunferência.
6 - Comece a reduzir o raio da circunferência, até que um ponto da figura passe pela circunferência. Este será o seu ponto P(x1,y1). Faça todas as futuras circunferências passarem por este ponto.
7 - Agora você vai variar o centro P(a,b) da circunferência.
Escolha novos valores de R, de modo a reduzir o raio. Para cada valor, calcule o novo ponto do centro da circunferência P(a,b).
Verifique se um segundo ponto coincide com a sua imagem. Você terá que usar um processo interativo, pois você deseja que a coincidência (ponto P(x2,y2)) coincida com o ponto mais afastado da sua imagem. Aí você descobriu o seu segundo ponto.
8 - Falta descobrir o terceiro ponto.
Trace uma reta (y = mx + c) que passe pelo seu ponto central atual P(a,b) e que passe também pelo centro da semi-reta que passa pelos pontos P1(x1, y2) e P2(x2,y2).
9 - Aumente ou diminua o raio R da circunferência, de modo que o centro da mesma coincida com um ponto da reta criada.
Para cada opção, verifique se ocorre uma coincidência com um ponto de sua imagem. A idéia é alterar o raio até que você encontre o terceiro ponto P3(x3,y3). Logicamente este ponto será o que ocorre com o maior raio, cuja circunferência ainda coincida com a imagem.
O ponto P(a,b) calculado será também o ponto central de sua imagem.
Este é o ponto de partida para saber se sua imagem é simétrica.
A partir daí, você deve criar retas que passam por este ponto e que possuam ângulos diferentes.
Para cada reta calcule dois pontos opostos ao ponto P(a,b) e que possuam a mesma distância.
Faça isso para muitos pontos e para muitas retas.
Para cada ponto duplo, veja se neles a imagem coincide.
Caso haja coincidência em todos eles, então sua imagem é simétrica.
Comece com um teste com um quadrado, para saber se o seu programa está correto.



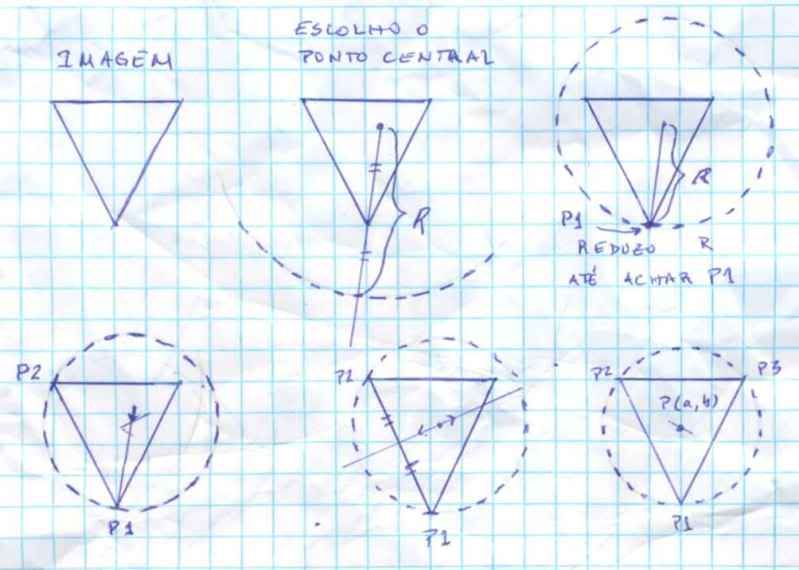
Com este procedimento sua imagem poderá ter qualquer formato.

MOR_AL

[Jorge_Francisco]

Faz o preenchimento do objeto de acordo com a luminancia ou outro método, faz uma binarização. Depois faz uma varredura em alguns angulos(imagino que o objeto esteja sempre em algum angulo prédefinido, senão atrapalha). Depois é só dividir ao meio e fazer uam estatística de pixels, nunca darão 99%, por questões de amostragem, mas pelo menos 90% irá dar. Claro que falei muito por alto, estou sem tempo aqui, senão te passava um programinha que fiz que detectava a face, desenha uma elipse no rosto, e traçava uma linha no meio da face de acordo com a inclinação da cabeça.

Abraço.

[joao]

Obrigado pelas dicas MOR_AL e Jorge_francisco.

Para quem nao estava começando a perder os poucos cabelos, agora posso pensar em colar eles novamente!

As dicas são muito boas, acho que agora consigo fazer com que o projeto ande. Ele tava parado desde janeiro, não só por causa deste algoritmo, mas por outras coisas. Mas pelo menos ele dá animo para continuar!

To começando a fazer agora. Depois coloco o resultado.

[]'s

[jeanfernandes]

Trabalhar com formas geometricas definidas por lados em linhas retas eh mole ne Joao.

Uma coisa que voce vai perceber nisso eh que a imagem scaneada vai ter pontos meio chatinhos fora da resolucao....e desta forma voce vai ter que procurar uma linearidade dos pontos fora da curva....

Magina que voce scaneou a borda do livro...o calculo dos pontos dos lados nem sempre vai cair numa equacao perfeita, entre dois vertices que teoricamente determina uma reta....

Em tese voce precisa descobrir os vertices e primeiramente verificar o processo de normalizacao dos pontos entre os vertices para deixar a figura mais bonitinha....

Caso a figura seja formada por uma reta + uma curva (tipo um circulo torado no meio....ce ta f****.....

Acho que o problema nao eh tao trivial assim nao....depende ate do angulo em que voce capta a parada....

existem algumas regras basicas....por exemplo...
determinados os vertices e normalizadas as arestas...e por fim de terminando que o poligono nao tem curvas fora de y = ax + b...ai vai algumas dicas basicas ne poe a coisa no plano cartesiano....

(sem pensar muito mas me corrija depois)
se todos os lados forem diferentes nao ha simetria.
se o poligono tem 2n + 1 lados (impar) ...tem que ter pelo menos n/2 pares de lados iguais....
se o poligono tem 2n (par) tem que ter (n-1) lados iguais... acho que eh isso ou alguma coisa perto disso....
tem que ver adjacencia dos lados e tals....

Outra coisa, se um poligono de 2n tiver 4 ou mais lados e for regular entao existem varias maneiras de achar a simetria ne (imagina um hexagono regular).

Entao nao eh tao direto o quanto voce pensa....

[joao]

Ola Jean!

Olha, eu só dei o livro como exemplo, imagina agora celulas, que de certa forma serão redondas(sei que vai ter ruido). Mas por isso mesmo eu vou usar um sistema que contenha margem de erro para as imagens.

O que o pessoal falou e o que eu acho que estah correto é:
- A imagem vai formar um quadrado, desde que vc pegue os maximos valores para cima, baixo, esquerda, direita.
- Se a imagem for simetrica, com certeza o centro será o centro do quadrado ou pelo menos, qualquer linha que corte atraves do centro do quadrado irá dar um corte na imagem que será o correto para a simetria. Se eu estiver errado, por favor, me mostre uma imagem simétrica que o centro do quadrado nao tenha uma linha que corte a imagem de forma simetrica. Ontem eu tentei imaginar um caso desses e não consegui achar. Entao, se alguem souber de algum caso que nao seja, eu agradeço bastante.
- Agora, se eu pegar o ponto superior esquerdo e o canto inferior direito do quadrado e ir "andando" pixel por pixel, verificando se a imagem é simetrica, até que a reta fique invertida(180 graus), eu testarei todos os possiveis resultados.

Então, a jogada está na criação do centro da imagem. Eu acho que não existe imagem simétrica que o centro do quadrado gerada por ela não dará em uma linha que corte a imagem.

E continuamos a discussão!


[]'s

[joao]

Ola Pessoal,

Acho que estou começando a ficar velho...
Não consigo resolver um probleminha simples(eu acho pelo menos) de geometria analitica

Olha só, eu quero achar o ponto que fica exatamente oposto a um ponto da reta. Exemplificando: tenho 1 ponto 1,1 e seu ponto oposto(como se fosse visto no espelho) seria -1,1, caso se use a reta do eixo Y como sendo a reta a ser seguida. Caso se usa-se a reta do eixo X, seria 1,-1.

Agora imagine que a reta que eu to usando esta inclinada....
Este é o meu problema. Eu tenho dois pontos P1, P2 que formam esta reta, que pode estar inclinada ou nao e tenho 1 ponto P que gostaria que fosse espelhado para o outro lado da reta.

Sei que é algo relacionado com retas perpendiculares, mas isso está me dando um banho!!! Cada vez mais que eu leio, parece que eu entendo menos ainda.


Se puderem me ajudar, agradeço!

[]'s

[albertorcneto]

Retas perpendiculares o coeficiente que multiplica eh o inverso do oposto. Ou seja, para achar uma reta perpendicular a y = ax + b voce deve usar a equacao y' = x/a + c, onde c pode ser qualquer valor que sera somente um offset. Se voce quiser que essa reta perpendicular passe por um ponto especifico da reta y = ax + b, com coordenadas Px e Py, entao c = aPx + b - Px/a.

Mas ainda nao entendi o que voce quer: voce quer uma reta espelhada ou um ponto espelhado? Se for um ponto, voce ja matou a charada. Se for uma reta, ela nao necessariamente vai ser perpendicular a original. Mas basta ter dois pontos dela pra calcular a equacao dela. Ex:

Se voce tem P1 e P2 da reta original, basta calcular P1' e P2' espelhados. Entao calcula-se os coeficientes a=(P1'y-P2'y)/(P1'x-P2'x) e b=P1'y - aP1'x.

[joao]

Ola Alberto!

Eu quero apenas 1 ponto espelhado.

Acho mais facil explicar com este simples exemplo:

Eu tenho a reta a um angulo de 45 graus com o eixo x e y. Entao supomos que dois pontos desta reta seriam: P1 = -10,10 e P2 = 9,-9. Ok? Reta bem simples, que passa também no ponto 0,0 mas preferi nao colocar este ponto, logo, o 0,0 eu nao tenho e também nem irá fazer falta.

Eu tenho ainda o ponto P que é 2,2. OK? Espelhando ele na reta acima, eu sei que o seu ponto oposto é P'= -2,-2. Isso é o que eu quero saber.

Agora, o que eu te pergunto e eu sei que vc explicou ali emcima, mas nao consegui ainda entender, é: como tendo os dados P1, P2 e P, eu consigo chegar no ponto P'.

[]'s

[Djalma Toledo Rodrigues]

Mas, se apenas um ponto então não seria preferível Coordenadas
Cartesianas ?
(X vezes -1) Y = Ponto espelhado

Ou Coordenadas Polares?
se transforma em um número complexo.